Distribusjonen av antall steg til Kaprekars konstant

Vi prøver Kaprekar’s rutine.

Jeg velget et firesifret tall, med minst to ulike siffer: 2345. Vi finner størst mulig variant 5432 og minst mulig variant 2345 fra sifrene og begynner rutinen…

5432 - 2345 = 3087
8730 - 0378 = 8352
8532 - 2358 = 6174

Vi har kommet frem til Kaprekar’s konstant: 6174 etter 3 steg

Dette er greit. Hvis jeg gjør dette på alle mulige fire-sifrede tall fordeler antall steg som må til før 6174 nås slik:

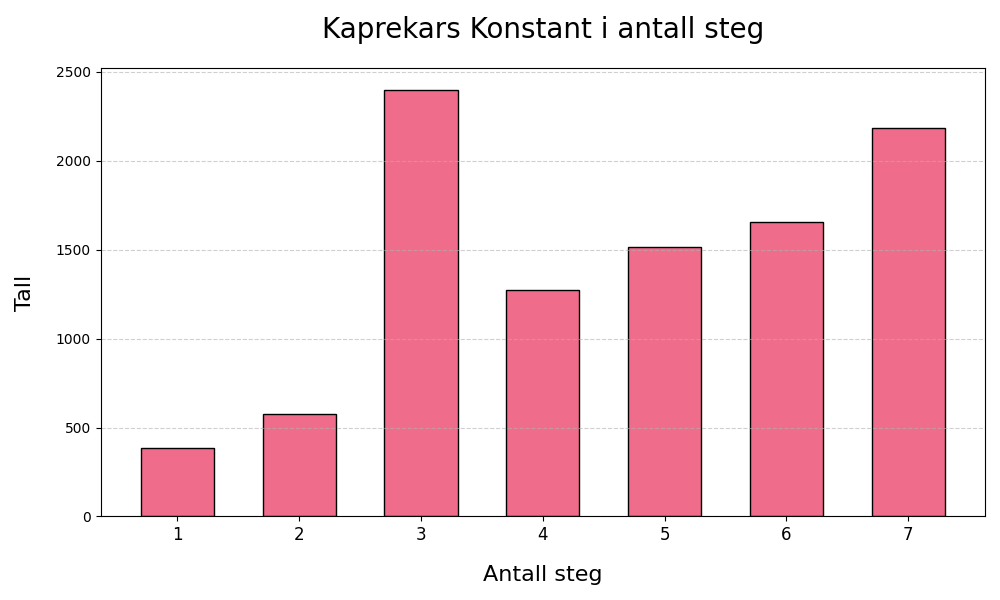
Denne fordelingen virker litt underlig og ikke helt ituitivt. Jeg føler umiddelbart at fordelingen burde vært mer jevn tvers over.

Kanskje ikke like jevnt, men jeg tenker at ett steg burde være sjeldnere enn syv steg, burde det ikke? Det har med utregningen å gjøre, Det er et begrenset antall kombinasjoner der resultatet blir 6174 på første forsøk. Det føles litt selvfølgelig og stemmer med diagrammet over. Den stiger sakte oppover mot syv steg, er det å forvente?

Det jeg finner mest underlig er at tre steg topper alle andre. Hvorfor det? Hvorfor er det så stor overvekt på tre? Hva betyr det? Dette skulle jeg gjerne funnet en forklaring på.